前言 排序算法是最基础也最重要的算法,故在此篇文章中对常用的几种排序算法进行总结,并列出其代码实现。
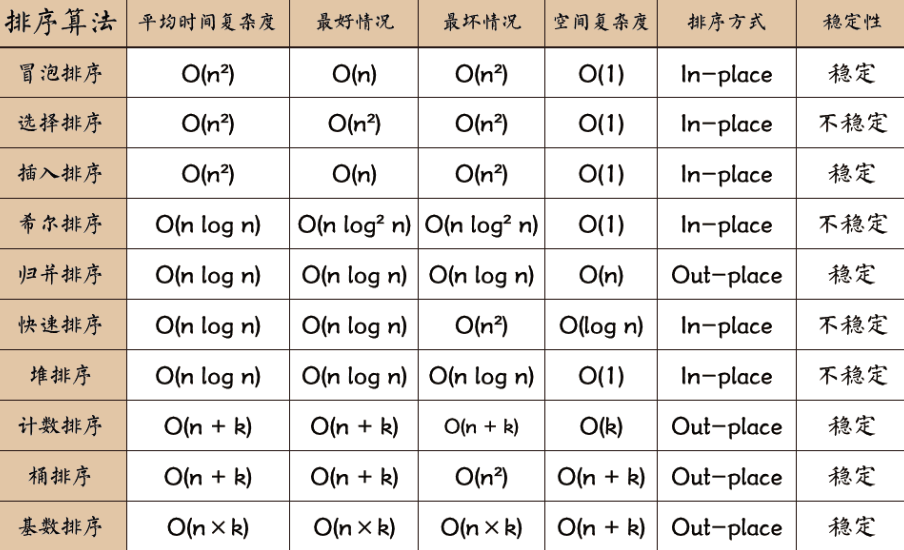
排序算法 排序算法可以分为内部排序 (In-place )和外部排序 (Out-place ):内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序 等。
稳定性 是指相等的元素经过排序之后相对顺序是否发生了改变。拥有稳定性这一特性的算法会让原本有相等键值的纪录维持相对次序,即如果一个排序算法是稳定的,当有两个相等键值的纪录 A 和 B,且在原本的列表中 A 出现在 B 之前,在排序过的列表中 A 也将会是在 B 之前。
其中,n 通常代表输入数据规模 ;k 代表与输入数据的取值范围或其他特定属性 相关的数值,比如桶排序中 k 为桶的大小。
下面就对这十种排序方法依次进行介绍:
冒泡排序 冒泡排序是最简单的排序算法之一,它通过重复地比较相邻元素,并根据需要交换它们来排序。这个算法的名字由来即是因为最小的元素会经由交换慢慢“浮”到数列的顶端。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public class BubbleSort { public static void bubbleSort (int [] arr) { int n = arr.length; for (int i = 0 ; i < n - 1 ; i++) { for (int j = 0 ; j < n - i - 1 ; j++) { if (arr[j] > arr[j + 1 ]) { int temp = arr[j]; arr[j] = arr[j + 1 ]; arr[j + 1 ] = temp; } } } } }
选择排序 选择排序通过反复找到剩余未排序部分的最小(或最大)元素,并将其放到正确位置。每次选择最小的元素,然后和当前的起始位置交换。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public class SelectionSort { public static void selectionSort (int [] arr) { int n = arr.length; for (int i = 0 ; i < n - 1 ; i++) { int minIdx = i; for (int j = i + 1 ; j < n; j++) { if (arr[j] < arr[minIdx]) { minIdx = j; } } int temp = arr[minIdx]; arr[minIdx] = arr[i]; arr[i] = temp; } } }
插入排序 插入排序通过将每个元素插入到它在已排序部分的正确位置来排序。对于每个元素,它从右向左遍历,找到合适的位置进行插入。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 public class InsertionSort { public static void insertionSort (int [] arr) { int n = arr.length; for (int i = 1 ; i < n; i++) { int key = arr[i]; int j = i - 1 ; while (j >= 0 && arr[j] > key) { arr[j + 1 ] = arr[j]; j = j - 1 ; } arr[j + 1 ] = key; } } }
希尔排序 希尔排序是插入排序的改进版本。它通过对远间隔的元素进行比较和交换来减少元素的移动次数,最终逐步缩小间隔,直到间隔为 1 时完成排序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public class ShellSort { public static void shellSort (int [] arr) { int n = arr.length; for (int gap = n / 2 ; gap > 0 ; gap /= 2 ) { for (int i = gap; i < n; i++) { int key = arr[i]; int j = i; while (j >= gap && arr[j - gap] > key) { arr[j] = arr[j - gap]; j -= gap; } arr[j] = key; } } } }
归并排序 归并排序是基于分治法的排序算法。它将数组分成两个子数组,分别排序后再将它们合并成一个有序数组。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 public class MergeSort { public static void mergeSort (int [] arr, int l, int r) { if (l < r) { int m = l + (r - l) / 2 ; mergeSort(arr, l, m); mergeSort(arr, m + 1 , r); merge(arr, l, m, r); } } public static void merge (int [] arr, int l, int m, int r) { int n1 = m - l + 1 ; int n2 = r - m; int [] L = new int [n1]; int [] R = new int [n2]; for (int i = 0 ; i < n1; i++) L[i] = arr[l + i]; for (int j = 0 ; j < n2; j++) R[j] = arr[m + 1 + j]; int i = 0 , j = 0 ; int k = l; while (i < n1 && j < n2) { if (L[i] <= R[j]) { arr[k] = L[i]; i++; } else { arr[k] = R[j]; j++; } k++; } while (i < n1) { arr[k] = L[i]; i++; k++; } while (j < n2) { arr[k] = R[j]; j++; k++; } } }
快速排序 快速排序是另一种基于分治法的排序算法。它通过选择一个基准元素,并将数组分为比基准小和比基准大的两部分,然后递归地对两部分进行排序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public class QuickSort { public static void quickSort (int [] arr, int low, int high) { if (low < high) { int pi = partition(arr, low, high); quickSort(arr, low, pi - 1 ); quickSort(arr, pi + 1 , high); } } public static int partition (int [] arr, int low, int high) { int pivot = arr[high]; int i = (low - 1 ); for (int j = low; j < high; j++) { if (arr[j] < pivot) { i++; int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } int temp = arr[i + 1 ]; arr[i + 1 ] = arr[high]; arr[high] = temp; return i + 1 ; } }
堆排序 堆排序是一种基于堆数据结构的比较排序算法。首先构建最大堆(或最小堆),然后将堆顶元素与最后一个元素交换并重新调整堆结构,直到整个数组有序。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 public class HeapSort { public static void heapSort (int [] arr) { int n = arr.length; for (int i = n / 2 - 1 ; i >= 0 ; i--) { heapify(arr, n, i); } for (int i = n - 1 ; i >= 0 ; i--) { int temp = arr[0 ]; arr[0 ] = arr[i]; arr[i] = temp; heapify(arr, i, 0 ); } } public static void heapify (int [] arr, int n, int i) { int largest = i; int left = 2 * i + 1 ; int right = 2 * i + 2 ; if (left < n && arr[left] > arr[largest]) largest = left; if (right < n && arr[right] > arr[largest]) largest = right; if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; heapify(arr, n, largest); } } }
计数排序 计数排序适用于元素范围有限的整数排序。它通过计算每个元素出现的次数来确定其在排序后数组中的位置。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public class CountingSort { public static void countingSort (int [] arr) { int max = Arrays.stream(arr).max().getAsInt(); int min = Arrays.stream(arr).min().getAsInt(); int range = max - min + 1 ; int [] count = new int [range]; int [] output = new int [arr.length]; for (int i = 0 ; i < arr.length; i++) { count[arr[i] - min]++; } for (int i = 1 ; i < count.length; i++) { count[i] += count[i - 1 ]; } for (int i = arr.length - 1 ; i >= 0 ; i--) { output[count[arr[i] - min] - 1 ] = arr[i]; count[arr[i] - min]--; } for (int i = 0 ; i < arr.length; i++) { arr[i] = output[i]; } } }
桶排序 桶排序将元素分散到几个桶中,然后分别对每个桶进行排序,最后将所有桶中的元素合并。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public class BucketSort { public static void bucketSort (int [] arr, int bucketCount) { if (arr.length == 0 ) return ; int max = Arrays.stream(arr).max().getAsInt(); int min = Arrays.stream(arr).min().getAsInt(); int range = (max - min) / bucketCount + 1 ; List<Integer>[] buckets = new List [bucketCount]; for (int i = 0 ; i < bucketCount; i++) { buckets[i] = new ArrayList <>(); } for (int i : arr) { int bucketIndex = (i - min) / range; buckets[bucketIndex].add(i); } int index = 0 ; for (List<Integer> bucket : buckets) { Collections.sort(bucket); for (int num : bucket) { arr[index++] = num; } } } }
基数排序 基数排序是一种非比较型排序算法。它按照个位、十位、百位等顺序逐步排序,每一位的排序使用稳定的排序算法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 import java.util.Arrays;public class RadixSort { public static void radixSort (int [] arr) { int max = Arrays.stream(arr).max().getAsInt(); for (int exp = 1 ; max / exp > 0 ; exp *= 10 ) { countingSortByDigit(arr, exp); } } public static void countingSortByDigit (int [] arr, int exp) { int [] output = new int [arr.length]; int [] count = new int [10 ]; for (int i = 0 ; i < arr.length; i++) { count[(arr[i] / exp) % 10 ]++; } for (int i = 1 ; i < 10 ; i++) { count[i] += count[i - 1 ]; } for (int i = arr.length - 1 ; i >= 0 ; i--) { output[count[(arr[i] / exp) % 10 ] - 1 ] = arr[i]; count[(arr[i] / exp) % 10 ]--; } for (int i = 0 ; i < arr.length; i++) { arr[i] = output[i]; } } }
参考文章 CSDN - 各种排序算法总结(全面)